README

The gellipsoid package extends the class of geometric ellipsoids to “generalized ellipsoids”, which allow degenerate ellipsoids that are flat and/or unbounded. Thus, ellipsoids can be naturally defined to include lines, hyperplanes, points, cylinders, etc. The methods can be used to represent generalized ellipsoids in a $d$ -dimensional space $\mathbf{R}^d$ , with plots in up to 3D.

The goal is to be able to think about, visualize, and compute a linear transformation of an ellipsoid with central matrix $\mathbf{C}$ or its inverse $^{-1}$ which apply equally to unbounded and/or degenerate ellipsoids. This permits exploration of a variety to statistical issues that can be visualized using ellipsoids as discussed by Friendly, Fox & Monette (2013), Elliptical Insights: Understanding Statistical Methods Through Elliptical Geometry doi:10.1214/12-STS402.

The implementation uses a $(\mathbf{U}, \mathbf{D})$ representation, based on the singular value decomposition (SVD) of an ellipsoid-generating matrix, $= ^{T}$ , where $\mathbf{U}$ is square orthogonal and $\mathbf{D}$ is diagonal.

For the usual, “proper” ellipsoids, $\mathbf{A}$ is positive-definite so all elements of $\mathbf{D}$ are positive. In generalized ellipsoids, $\mathbf{D}$ is extended to non-negative real numbers, i.e. its elements can be 0, Inf or a positive real.

Definitions

A proper ellipsoid in $\mathbf{R}^d$ can be defined by $:= \x \ : \ x^T x \$ where $\mathbf{C}$ is a non-negative definite central matrix, In applications, $\mathbf{C}$ is typically a variance-covariance matrix A proper ellipsoid is bounded, with a non-empty interior. We call these fat ellipsoids.

A degenerate flat ellipsoid corresponds to one where the central matrix $\mathbf{C}$ is singular or when there are one or more zero singular values in $\mathbf{D}$ . In 3D, a generalized ellipsoid that is flat in one dimension ( $= \X, X, 0\$ ) collapses to an ellipse; one that is flat in two dimensions ( $= \X, 0, 0\$ ) collapses to a line, and one that is flat in three dimensions collapses to a point.

An unbounded ellipsoid is one that has infinite extent in one or more directions, and is characterized by infinite singular values in $\mathbf{D}$ . For example, in 3D, an unbounded ellipsoid with one infinite singular value is an infinite cylinder of elliptical cross-section.

Principal functions

Installation

# install.packages("devtools")
devtools::install_github("friendly/gellipsoid")

Example

Properties of generalized ellipsoids

The following examples illustrate gell objects and their properties. Each of these may be plotted in 3D using ell3d(). These objects can be specified in a variety of ways, but for these examples the span is simplest.

library(gellipsoid)
(zsph <- gell(Sigma = diag(3)))  # a unit sphere in R^3
#> $center
#> [1] 0 0 0
#> 
#> $u
#>      [,1] [,2] [,3]
#> [1,]    0    0    1
#> [2,]    0    1    0
#> [3,]    1    0    0
#> 
#> $d
#> [1] 1 1 1
#> 
#> attr(,"class")
#> [1] "gell"
signature(zsph)
#>  pos zero  inf 
#>    3    0    0
isBounded(zsph)
#> [1] TRUE
isFlat(zsph)
#> [1] FALSE

(zplane <- gell(span = diag(3)[, 1:2]))  # a plane
#> $center
#> [1] 0 0 0
#> 
#> $u
#>      [,1] [,2] [,3]
#> [1,]    1    0    0
#> [2,]    0    1    0
#> [3,]    0    0    1
#> 
#> $d
#> [1] Inf Inf   0
#> 
#> attr(,"class")
#> [1] "gell"
signature(zplane)
#>  pos zero  inf 
#>    0    1    2
isBounded(zplane)
#> [1] FALSE
isFlat(zplane)
#> [1] TRUE

dual(zplane)  # line orthogonal to that plane
#> $center
#> [1] 0 0 0
#> 
#> $u
#>      [,1] [,2] [,3]
#> [1,]    0    0    1
#> [2,]    0    1    0
#> [3,]    1    0    0
#> 
#> $d
#> [1] Inf   0   0
#> 
#> attr(,"class")
#> [1] "gell"
signature(dual(zplane))
#>  pos zero  inf 
#>    0    2    1

A hyperplane. Note that the gell object with a center contains more information than the geometric plane.

(zhplane <- gell(center = c(0, 0, 2), 
                 span = diag(3)[, 1:2]))  # a hyperplane
#> $center
#> [1] 0 0 2
#> 
#> $u
#>      [,1] [,2] [,3]
#> [1,]    1    0    0
#> [2,]    0    1    0
#> [3,]    0    0    1
#> 
#> $d
#> [1] Inf Inf   0
#> 
#> attr(,"class")
#> [1] "gell"
signature(zhplane)
#>  pos zero  inf 
#>    0    1    2

dual(zhplane)  # orthogonal line through same center
#> $center
#> [1] 0 0 2
#> 
#> $u
#>      [,1] [,2] [,3]
#> [1,]    0    0    1
#> [2,]    0    1    0
#> [3,]    1    0    0
#> 
#> $d
#> [1] Inf   0   0
#> 
#> attr(,"class")
#> [1] "gell"

zorigin <- gell(span = cbind(c(0, 0, 0)))
signature(zorigin)
#>  pos zero  inf 
#>    0    3    0

# what is the dual (inverse) of a point?
dual(zorigin)
#> $center
#> [1] 0 0 0
#> 
#> $u
#>      [,1] [,2] [,3]
#> [1,]    0    0    1
#> [2,]    0    1    0
#> [3,]    1    0    0
#> 
#> $d
#> [1] Inf Inf Inf
#> 
#> attr(,"class")
#> [1] "gell"

signature(dual(zorigin))
#>  pos zero  inf 
#>    0    0    3

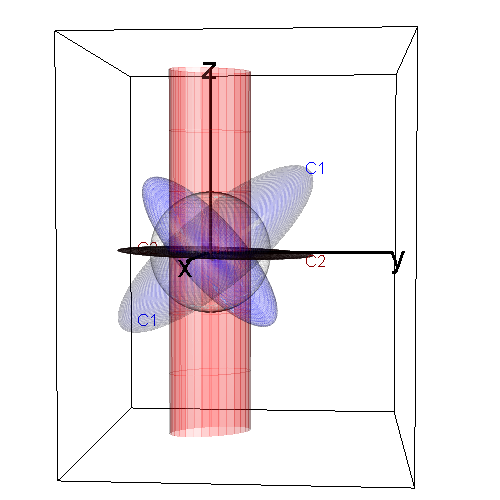
Drawing generalized ellipsoids

The following figure shows views of two generalized ellipsoids. $C_1$ (blue) determines a proper, fat ellipsoid; it’s inverse $C_1^{-1}$ also generates a proper ellipsoid. $C_2$ (red) determines an improper, flat ellipsoid, whose inverse $C_2^{-1}$ is an unbounded cylinder of elliptical cross-section. $C_2$ is the projection of $C_1$ onto the plane where $z = 0$ . The scale of these ellipsoids is defined by the gray unit sphere.

References

Friendly, M., Monette, G. and Fox, J. (2013). Elliptical Insights: Understanding Statistical Methods through Elliptical Geometry. Online paper

gellipsoid: Generalized Ellipsoids